Why Simplify page for printing is not available 2021 at all? It is not grey, just not available as option at all?
Why Simplify page for printing is not available 2021 at all? It is not grey, just not available as option at all?
الحل المُختار
Yes I saw both sections, the point I'm making regarding the printer choice is... The next time I use Firefox (Another day) why is the "Destination" dialogue showing the last printer I used and not the printer set as default on the computer?
With regard to the dialogue to set the pages to be printed... Aha! I see now, I have to click "Custom" to get at the required dialogue. So it looks like a brain fart on my part. :-(
Thanks for the info, appreciated. Ax
Read this answer in context 👍 0All Replies (14)
Enter about:config in the URL bar and set the following preferences:
- print.use_simplify_page = true
- print.tab_modal.enabled = false
"Simplify Page" applied Reader View to the old Print Preview layout for printing purposes. However with the new experience, if you apply Reader View to the page before hitting Ctrl+P, that carries over to printing automatically. So a "Simplify Page" feature in the print overlay is redundant, unless you only want to apply Reader View to printouts and not to the document on screen.
There is a bug on file to accommodate the latter scenario (perhaps in Firefox 86), but for now, hopefully triggering Reader View before printing will work for you.
Or rolling back to the old experience.
Thanks Ty!!! Worked perfectly. Would have never figured it out. Print preview is exactly like it used to be. Much appreciated!!!
I had this one correct > print.use_simplify_page = true ...but not this one > print.tab_modal.enabled = false
Thanks Again! Ken
I ended up here after searching for a way to rid myself of the new Firefox print dialogue... The about:config solution works, so thanks for that. :-)
I have absolutely no idea what the other solution was about... Reader view ... Whatever that might be!
It is a worthy endeavour to improve the browser printing capabilities, but a couple of thing (At the least) need fixing with the new dialogue if it continues to exist.
1) The last printer used is assumed to be the default the next time Fx is used, so it doesn't read the machine's set default printer. I have multiple printers in use for different things and manually select them as required, only one is set as the system default, so unless the user is very careful, Fx will print to the wrong printer, wasting ink/toner.
2) In the new dialogue I could not find a config to control pages printed... Like, print pages 1-2 or even only print one page out of many like 4-4 it just ran away and printed the lot. Again wasting ink/toner. :-(
Ax
arturox said
I have absolutely no idea what the other solution was about... Reader view ... Whatever that might be!
Reader View is the component that simplifies page layouts for both on-screen viewing and for printing. See: Firefox Reader View for clutter-free web pages.
1) The last printer used is assumed to be the default the next time Fx is used, so it doesn't read the machine's set default printer. I have multiple printers in use for different things and manually select them as required, only one is set as the system default, so unless the user is very careful, Fx will print to the wrong printer, wasting ink/toner.
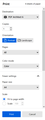
The new print experience is an improvement over the classic one when it comes to easily changing printers and seeing how the layout and settings are different from the last used printer. It is literally the first setting:

2) In the new dialogue I could not find a config to control pages printed... Like, print pages 1-2 or even only print one page out of many like 4-4 it just ran away and printed the lot.
See the above screenshot. Doesn't yours show that section?
الحل المُختار
Yes I saw both sections, the point I'm making regarding the printer choice is... The next time I use Firefox (Another day) why is the "Destination" dialogue showing the last printer I used and not the printer set as default on the computer?
With regard to the dialogue to set the pages to be printed... Aha! I see now, I have to click "Custom" to get at the required dialogue. So it looks like a brain fart on my part. :-(
Thanks for the info, appreciated. Ax
Modified
arturox said
Yes I saw both sections, the point I'm making regarding the printer choice is... The next time I use Firefox (Another day) why is the "Destination" dialogue showing the last printer I used and not the printer set as default on the computer?
Firefox has always worked this way. If you want Firefox to "reset" to default every time after printing, you need to toggle a preference:
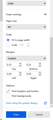
(1) In a new tab, type or paste about:config in the address bar and press Enter/Return. Click the button accepting the risk.
(2) In the search box in the page, type or paste save_p and pause while the list is filtered
(3) Double-click the print.save_print_settings preference to switch the value from true to false
Or is the problem that Firefox is ignoring that preference when you use the new overlay?
It seems to be ignoring the preference setting...
I've just applied the change to print.save_print_settings so it is "False". Manually selected a printer, say Epson Colour (Not the system default) and printed a Firefox page. After the page prints out okay...
Quit Firefox by Menubar-File-Exit
Run Firefox. Navigated to a page... Selected print, but the printer dialogue still contains the Epson Colour printer not the Win machine default a HP-Laserjet.
I've re-tested a couple of times using other printers I have available, and the end result is the same.
I've even rebooted the computer, and checked the default printer is the HP-Laserjet... It is.
So yes it is ignoring the set preference. :-( Thanks
Ax
What is wrong with redundancy in a user interface? It is a VIRTUE not a design flaw. Let users interact with the web according to their own preferences. Why should millions of Firefox Mozilla users have to re-adjust and re-learn basic interactions according to some random programmer's esthetic whim? I have never used Reader's View. I have tried the Simplify view within print preview to see whether it would be useful for a particular page I wish to print or save as a PDF vs. a text file. This 'improvement' is no improvement. I hate it when FireFox Mozilla imposes these major changes with no notification or option. I dread the Update Available notice that seem to come every week. Why do I have to master the internal workings of FF just to continue to be able to perform basic functions? AND tinker in about:config to un-do these 'improvements' ? Thank you for posting the names of the 'preferences' to change back - but it is frustrating that I have to do it at all. I am not a programmer. I don't find this enjoyable or interesting.
Please only email me to answer question said
What is wrong with redundancy in a user interface? It is a VIRTUE not a design flaw.
I don't think this is about redundancy. There is a request on file to add the Simplify Page checkbox to the new print experience in a future release. As a workaround for now you can use the Reader View button. To reduce the line spacing and font size, you can use the Reader View toolbar:

I am currently using print.tab_modal.enabled = false and print.use_simplifyPage=true. I also use the print preview extension. Reader View is NOT a substitute for Simplify Page.
I am very dependent on Simplify Page functionality: - To save on ink and paper. - To prevent strain when reading. I can't read everything on a screen.
One of the most important browser features for me is print capabilities and why I choose Firefox. I am hopeful Firefox will retain Simplify Page functionality in future releases.
I made the config entries above. I also went to View --> PAge Style --> Basic Page Style.
Under the new print dialogue, there is now no way to print this page (not JUST this page, but a good example) from Firefox: https://www.lenovo.com/us/en/laptops/thinkpad/thinkpad-x1/X1-Carbon-Gen-8-/p/20U9005MUS
All I am able to get is the first 2 pages. Previously, I was able to click "simplify page" and get everything. Even with the config edits, "simplify page" is grayed out
Hi ddmiller, Simplify Page is offered on the same pages that Reader View is offered on: they are pages that have an article-like layout that Firefox knows how to simplify. Many (most?) pages on the web do not have that kind of layout and cannot be simplified by Firefox. (Maybe they can be simplified/streamlined by an add-on.)
That particular page seems to completely befuddle Firefox...
Hi everyone,
arturox's post was marked as the solution by the person who asked the original question. Your issue may have similar symptoms, but it is likely a different cause/solution. For better help, it would be best to use https://support.mozilla.org/en-US/questions/new where volunteers can get more details about your setup.
Because this thread is solved and more people might start using it for their own questions, I'm going to lock it.